Chapter 3 Trip Distribution
The trip distribution model is the second component in a traditional 4-step model. The purpose of the trip distribution model is to produce a trip table with the estimated number of trips from each TAZ to every other TAZ in the study area. To do this, predicted productions at each origin TAZ, and predicted attractions at each destination TAZ are combined to create a production-attraction model. Your homework this week will focus on a basic, three zone system which you will calibrate using a Gravity Model. The Gravity Model assumes that the number of trips between any two zones is directly proportional to the trips produced and attracted, controlling for the proportional to the travel time between two zones.
Please reference this article from the Travel Forecasting Resource for more information about about trip distribution. Section 4.5 of NHCRP report 716 also provides good background.
Homework
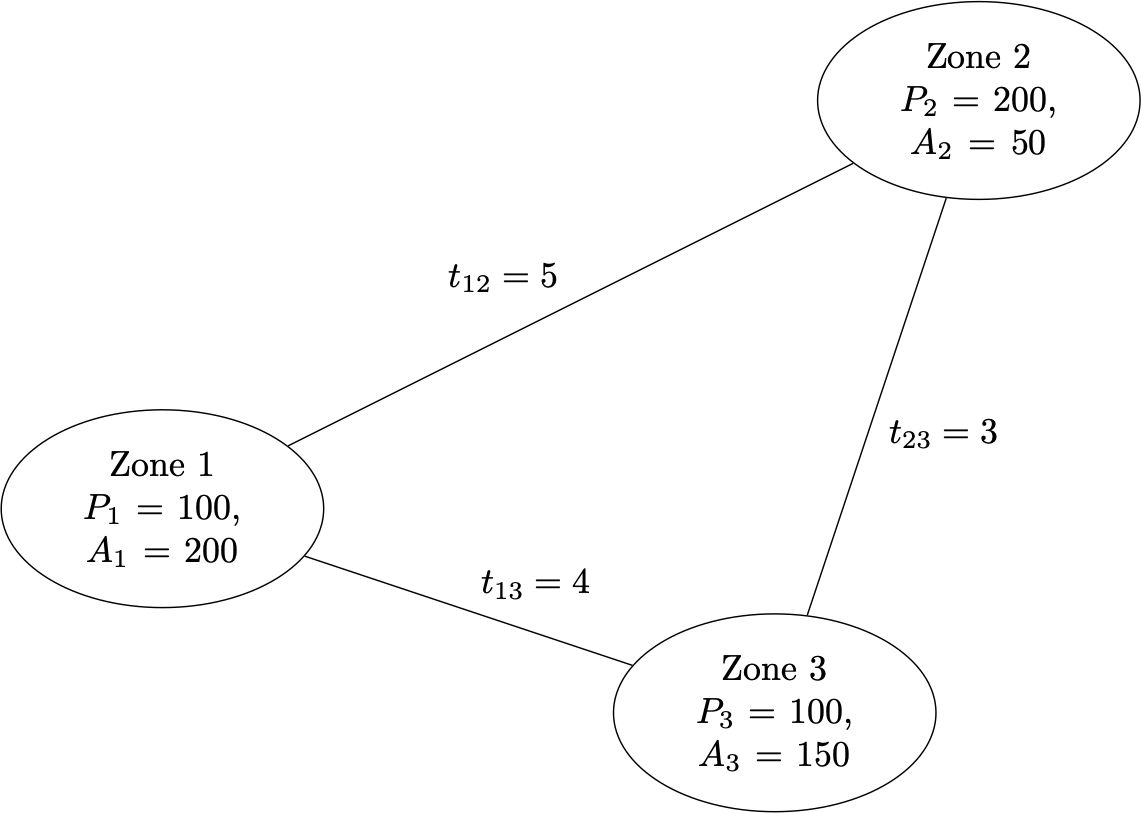
Figure 3.1: Simple 3-Zone System.
Figure 3.14 presents a simple three zone system, the link travel times for this system (for internal trips, \(t_{ii}=2\) globally), and the zonal productions and attractions. In this homework you will develop, calibrate, and apply a doubly-constrained gravity model for this system.
First Problem: Gravity Model Development
In this step, you will develop a gravity model. Assume a gravity model of the form
\[T_{ij}=\frac{P_iA_j^*(t_{ij})^{-b}}{\sum_{j'\in J}A^*_{j'}(t_{ij'})^{-b}}\]
where \(A_j^*\) is a “modified attraction term” defined by the algorithm shown in Figure 3.2 below. This is an iterative algorithm; in each iteration the \(A^*\) vector gets updated based on the difference between the predicted trips \(T_{ij}\) and the input attractions \(A\). As the number of iterations increases, the ratio \(A_j / \sum_i T_{ij}\) gets closer to 1. At the same time, the difference between successive predicted trip matrices becomes close to zero. This algorithm therefore “doubly-constrains” the predicted trips to a given zone to equal the input zonal attractions \(A_j\), within some tolerance represented by the value \(\varepsilon\).
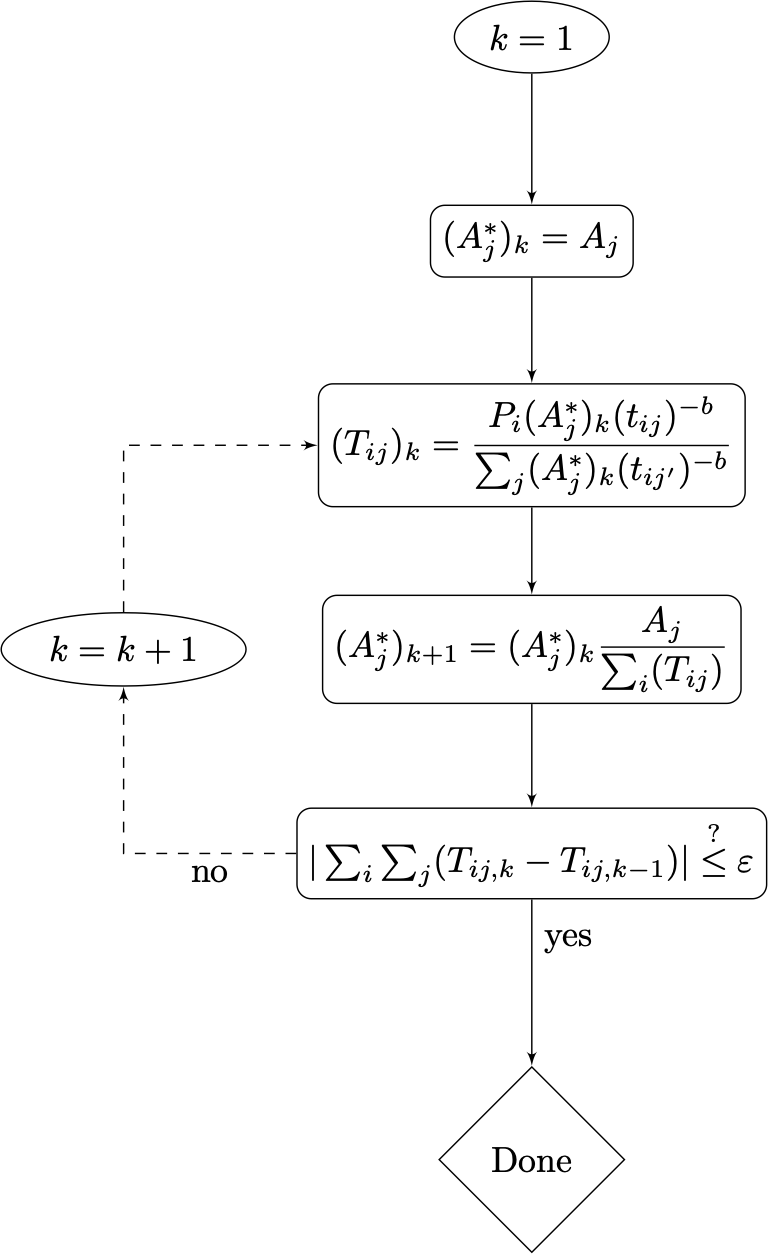
Figure 3.2: Trip balancing algorithm.
Why might we want to doubly-constrain a gravity model? Why might we not?
Write a program function or develop a spreadsheet to apply this doubly-constrained gravity model.
The function code below shows how to calculate one iteration of a gravity model in R. The function takes the production and attractions vector, in addition to the cost matrix and the impedance parameter, and calculates the \(T_{ij}\) matrix. Once you have this function (as well as the necessary vectors and cost matrix), you can calculate the gravity model with arbitrary values of the impedance coefficient.
#' Gravity Model
#' @param p vector of productions, length n
#' @param A vector of attractions, lenth n
#' @param C matrix of impedances, dim n x n
#' @param b impedance parameter
gravity <- function(p, a, C, b){
# output matrix (all 0 here)
trips <- matrix(0, nrow = length(p), ncol = length(a))
# loop over all rows (production)
for (i in 1:length(p)) {
bottomA <- sum(a * C[i, ]^(-b)) # denominator
# loop over all columns (attraction)
for (j in 1:length(a)) {
# calculate gravity model for trips from i to j
topA <- a[j] * C[i,j]^(-b)
trips[i, j] <- p[i] * topA / bottomA
}
}
return(trips)
}
# calculate one round of gravity model with
p <- c(100, 200, 100)
a <- c(200, 50, 150)
C <- matrix(c(2,5,4,5,2,3,4,3,2), nrow=3, byrow=TRUE)
gravity(p, a, C, b = 0.5)## [,1] [,2] [,3]
## [1,] 59.22613 9.364473 31.40940
## [2,] 84.61917 33.448665 81.93216
## [3,] 42.56523 12.287524 45.14725## [,1] [,2] [,3]
## [1,] 75.27793 4.760994 19.96108
## [2,] 55.52540 54.870858 89.60374
## [3,] 28.52074 10.977638 60.50162Note that were we not going to doubly-constrain this model, we would be done. But we now need to implement the algorithm presented in 3.2. We now have a model that at least generates a trip matrix that is constrained to the attractions.
#' Function to balance gravity model
#' @param p vector of productions, length n
#' @param A vector of attractions, lenth n
#' @param C matrix of impedances, dim n x n
#' @param b impedance parameter
#' @param tolerance Acceptable change in trips matrix
balance_gravity <- function(p, a, C, b, tolerance) {
# define starting values
k <- 0 #iteration counter
astar <- a # starting unadjusted attractions
trips0 <- matrix(0, nrow = length(p), ncol = length(a)) #initial T is 0's
error <- Inf # first time through, error is Infinite
# loop through algorithm
while(error > tolerance){
# compute gravity model with adjusted attractions, using your function
trips <- gravity(p, astar, C, b)
# calculate the error as the change in trips in successive iterations
error <- sum(abs(trips - trips0))
# protect against infinite loops, increment values
if (k > 100) break # maximum of 100 iterations
k <- k + 1
trips0 <- trips
astar <- astar * a / colSums(trips) # next iteration astar
}
return(trips)
}
double_constrained_trips <- balance_gravity(p, a, C, 0.5, 0.01)
double_constrained_trips## [,1] [,2] [,3]
## [1,] 62.50975 8.329009 29.16124
## [2,] 91.54031 30.492846 77.96684
## [3,] 45.94993 11.178146 42.87193## [1] 200 50 150Second Problem: Model Calibration
The three-zone system defined in Figure 3.1 has the observed trip matrix listed below. What we need to do now is find the value of \(b\) that minimizes the difference between the observed and predicted trip matrix. You could solve this manually by trying different values of beta, or by using a goal seek / optimization program. The choice is yours, but you should document what you do in your homework response. You also need to determine how you are calculating the “difference”: sum of absolute error? Root mean squared error, etc.
| \(i\) | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 80 | 5 | 15 |
| 2 | 80 | 40 | 80 |
| 3 | 40 | 5 | 55 |
Third Problem: Model Application
The region represented in Problem 1 has begun improvements to the link between zones 1 and 2 that will reduce the travel cost from 5 to 3. Using your algorithm and the value of \(b\) that you calibrated above, determine the effect of this improvement on the predicted trip distribution matrix. That is, change the cost matrix to represent the forecasted travel costs and re-run your doubly-constrained gravity model algorithm. Is the response reasonable?
This problem is adapted with permission from Urban Transportation Planning: Second Edition by Michael D. Meyer and Eric J. Miller.↩︎