3 Economics

You buy lots of things. From the shoes to your feet to the mask on your face, almost everything you can see or touch was purchased. If not by yourself, than by someone else. Some things you buy and then own. Other things you pay a fee to rent. Other things are services or experiences that you can buy.

You will also sell lots of things throughout your life. Obviously if you are in a trade that produces goods, you will sell those goods. There will also be occasions where you will sell something you are no longer using, be it a tennis racket at a yard sale, or a car you have replaced, or a home you no longer live in. But as an engineer the thing you will sell most frequently is your knowledge and skills through your labor. Someone will pay you for expertise and time that they do not have, and in exchange you will buy the things you and your family and your business need to keep going.

The sum total of all of these buying and selling transactions in a society is called the Economy, and economics is the branch of social science that studies these transactions. This chapter consists of lectures on wider economic principles. Note that information about “Engineering Economics” is contained in Chapter 4.

Think

Looking at the world from a purely economic perspective — the idea that anything in this world can be purchased with sufficient funds — is at once true and supremely corrupting / discouraging. Money is a necessary evil of our world, and it (almost) always has been. But understanding how the economy works is necessary to succeed in life and help yourself and those around you overcome the world. Some teachings on money from the Savior:

And I say unto you, Make to yourselves friends of the mammon of unrighteousness; that, when ye fail, they may receive you into everlasting habitations. — Luke 16:9 ¹

Lay not up for yourselves treasures upon earth, where moth and rust doth corrupt, and where thieves break through and steal: But lay up for yourselves treasures in heaven, where neither moth nor rust doth corrupt, and where thieves do not break through nor steal: For where your treasure is, there will your heart be also. —Matthew 6:19-20

3.1 Supply and Demand

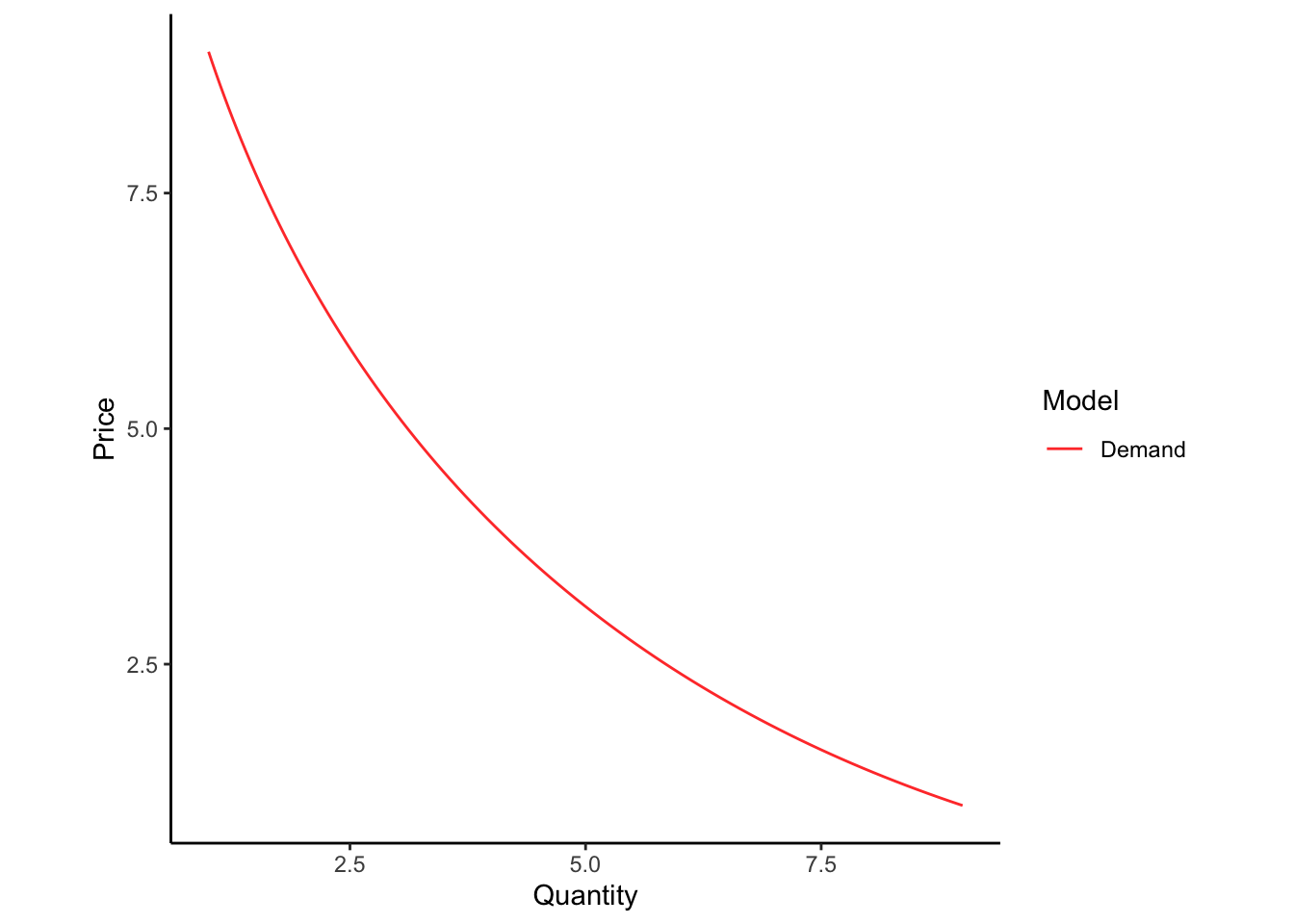
Let’s say people want to buy widgets. People will buy a certain number of them based on how much they cost. If the price is low, people will buy lots of widgets. If the price is high, people will not buy as many. This demand function $P = D(Q)$ might look like this:

The slope of the demand line is related to a meaningful economic concept called the elasticity. Mathematically, elasticity is defined as the percent change in the quantity demanded resulting from a percent change in the price.

\[ \varepsilon = \frac{\%\Delta Q}{\% \Delta p} \tag{3.1}\]

Example

When the price of gasoline was $2.45 per gallon, the average driver in Utah used 11.3 gallons per week. When the price increased to $2.55 per gallon, the average driver in Utah cut out a couple of unnecessary trips and used 11.2 gallons per week. What is the elasticity?

We just need to calculate the percent change in these values

\[\begin{align*} \varepsilon & = \frac{\%\Delta Q}{\% \Delta p}\\ &= \frac{(Q_1 - Q_0)/Q_0}{(P_1 - P_0)/P_0}\\ &= \frac{(Q_1 - Q_0)P_0}{(P_1 - P_0)Q_0}\\ &= \frac{(11.2- 11.3)2.45}{(2.55- 2.45)11.3}\\ &= -0.217 \end{align*}\]

Some goods are elastic, meaning that a small change in price results in a large change in demand, ($\varepsilon < -1$). Other goods are inelastic, meaning that demand will remain more or less fixed as the price goes up ($-1 < \varepsilon < 0$). Goods where the demand actually increases at the price goes up ($\varepsilon > 0$) exist, but are very unusual.

Think

Are there goods that you will buy no matter what the price is? For lots of people, things like milk, gasoline, and diapers fit in this category.

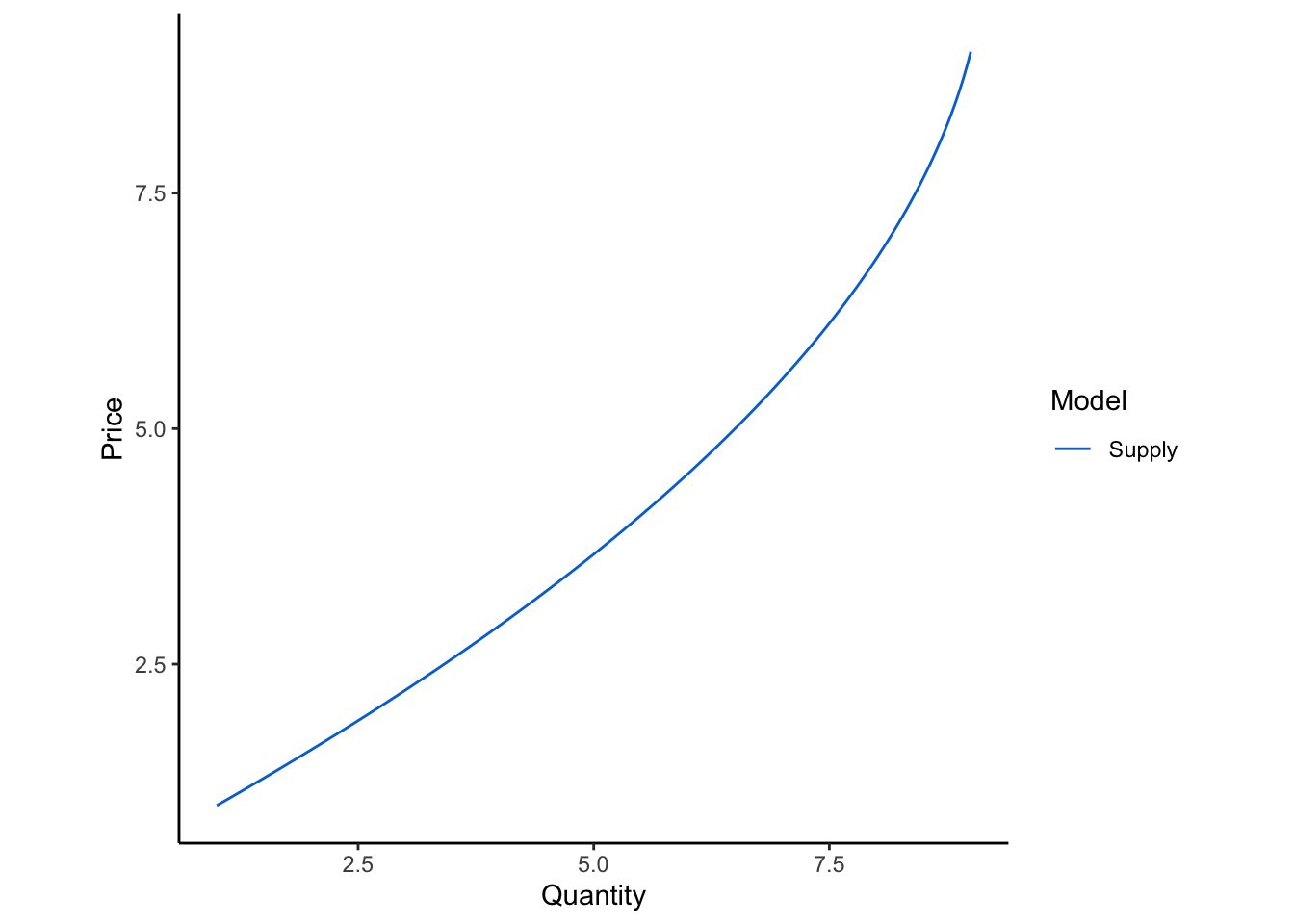
Somewhere else in the economy, there are people who make widgets. These people have exactly the opposite incentives as the people in the demand function. If the price of widgets is high, manufacturers will want to sell lots of them. If the price is low, then manufacturers will not make as many. This supply function $P = S(Q)$ looks like this:

When we put both functions on the same plot, you can see that there is a particular price where the demand and supply curves intersect. If manufacturers set a higher price than this equilibrium point, they will make more widgets than people will buy. If manufacturers set a lower price point, they will run out of inventory and lose revenue. Note that this solution also sets the quantity of goods that should be manufactured or purchased.

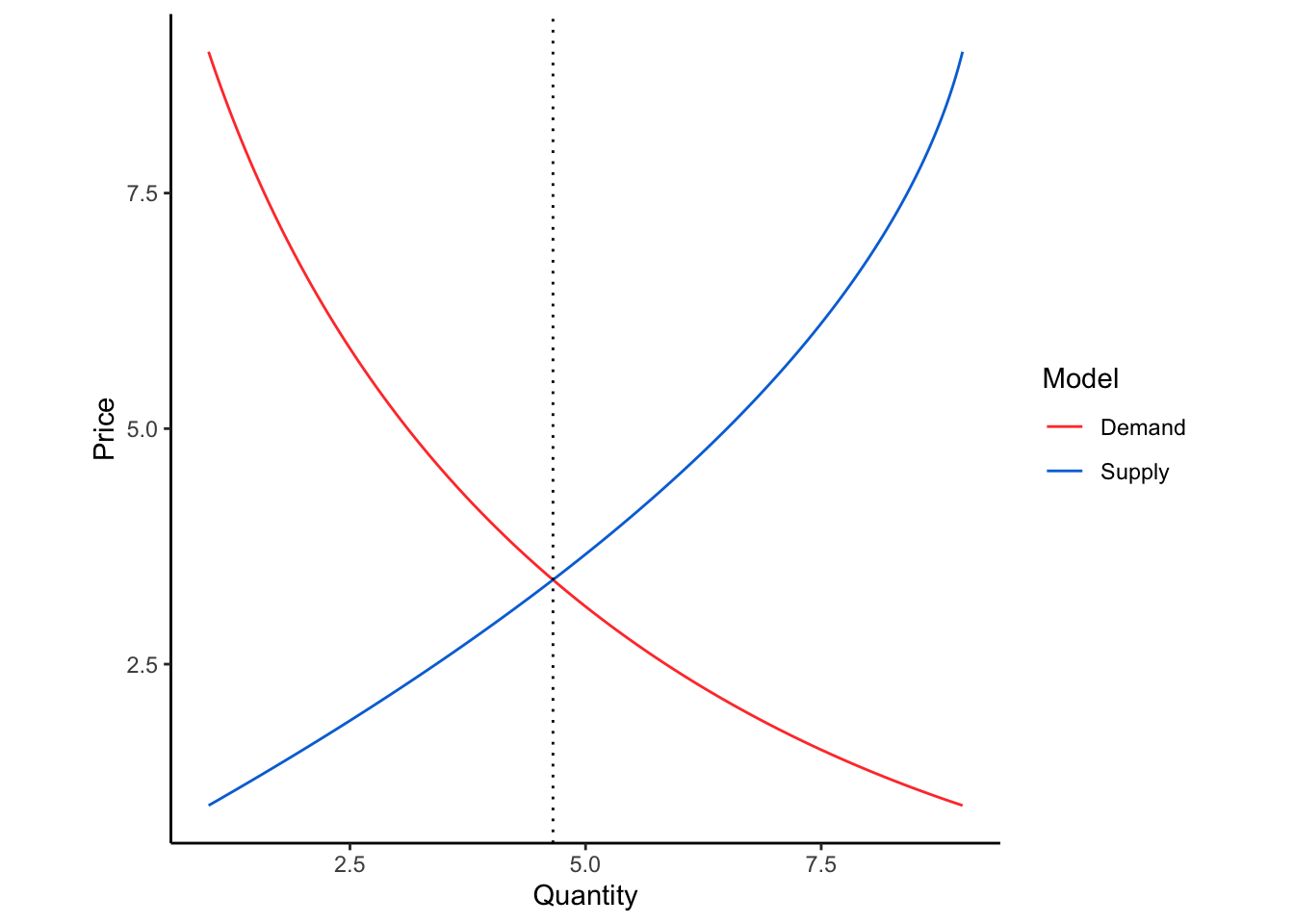
Finding the intersection of the supply and demand functions requires some simple algebra. You are looking for the solution $(Q, p)$ of the system of equations

\[ \begin{cases} p = S(Q) \\ p = D(Q) \end{cases} \tag{3.2}\]

This is most easily done by setting the difference of the functions equal to zero $S(Q) - D(Q) = 0$ and then solving one of the other equations for $p$.

Example

The demand for a good can be described by the function $p = 2/Q$. The supply of the good can be described by the function $p = 0.5Q$. What is the equilibrium price and the quantity sold / purchased?

We need to find the solution to these two functions.

\[\begin{align*} \frac{2}{Q} &= 0.5Q\\ 2 &= 0.5 Q^2\\ Q &= \sqrt{4}\\ &= 2 \end{align*}\]

And if $Q = 2$, then $p = 1$.

Supply and demand functions change over time. Sometimes the reason is obvious, and sometimes it is not. If the population grows, then there will be more people who want to buy widgets. This will push the demand for widgets upwards. If nothing else changes in the supply function, then the price will rise and more widgets will be produced / purchased.

If the population grows by 10%, a simplifying assumption would be that the entire demand curve also increases by 10%, $p = 1.1 * D(Q)$.

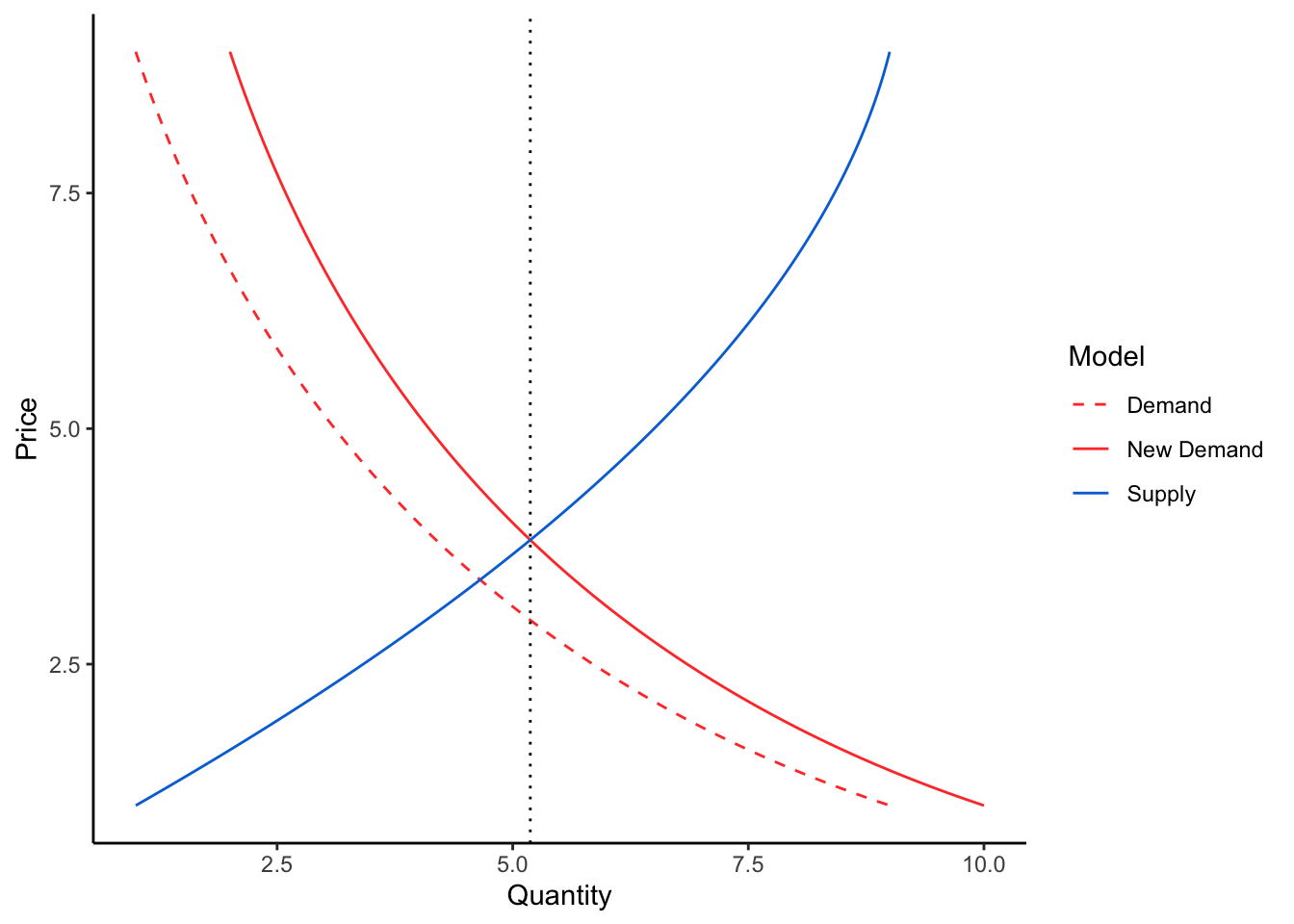
Sometimes the supply function will move up as well, meaning the system could reach the same equilibrium price for widgets as before. But often, the manufacturers have sufficient market power to increase supply while holding the price a little bit higher than before. This results in inflation, or the nominal price of goods creeping upwards. When wages increase to match price inflation, you have the tendency for currencies to lose purchasing power over time.

Think

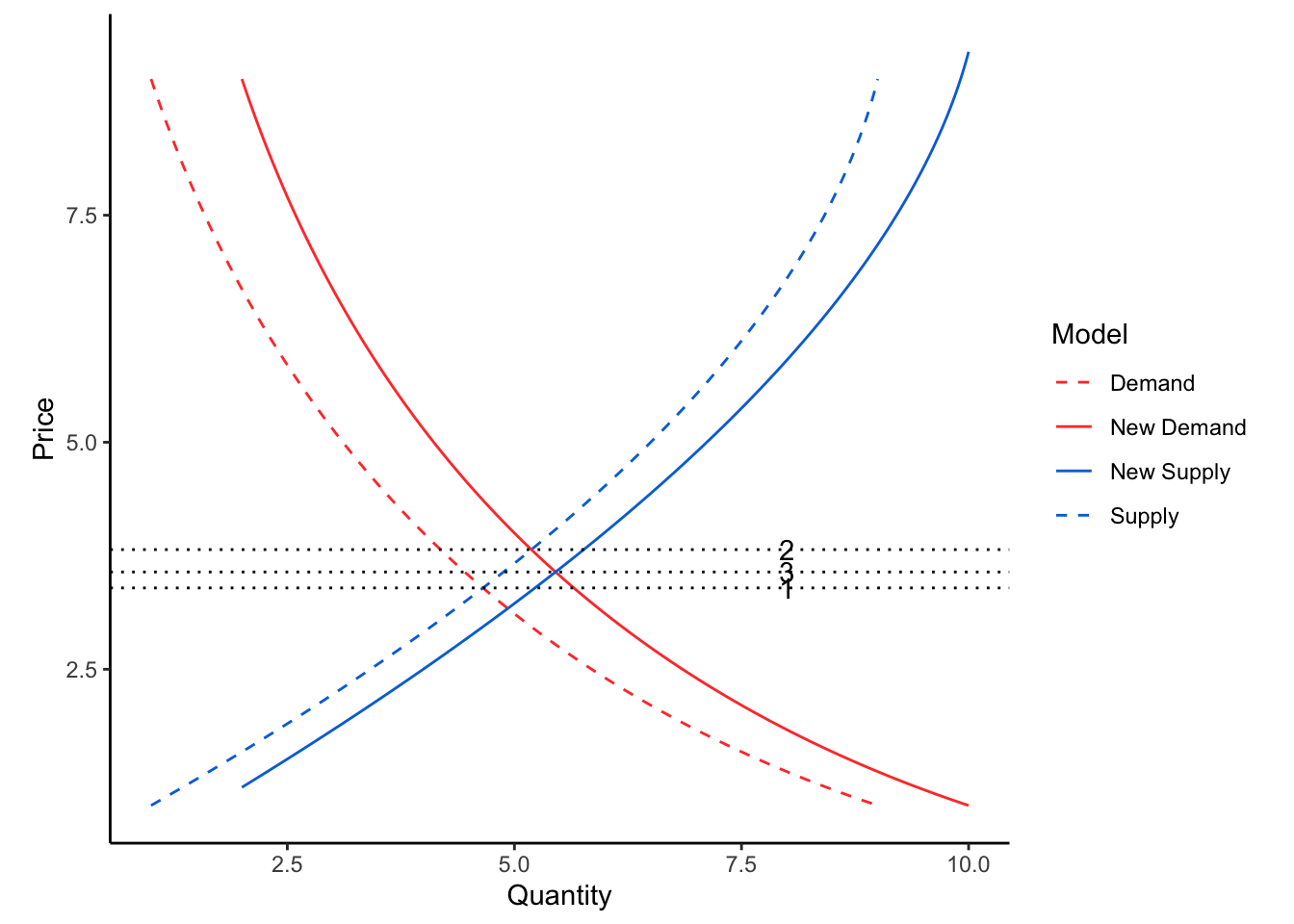
Inflation is often seen as a bad thing, because it means that a dollar you have now will not buy as much as in the future. But what happens when there is price deflation? Or what if inflation was exactly zero?

3.2 Comparative Advantage, Opportunity Cost, and Trade

It is not conceivable that one person could learn everything there is to know in this life. And even if someone tried, little time would be left for anything else. Everyone has unique talents, interests, and skills that they have developed. By selling skills and knowledge that you have to people that don’t, you can earn a living. Money is a key component in this. A university professor cannot easily purchase groceries by volunteering to lecture the checkout clerks. Instead, university students pay tuition² in exchange for a chance at a degree. The university then pays the professor a salary to teach and research, and the professor can then go to the grocery store and buy food for his or her family.

Of course, some people are better at doing some things than others. As much as a professor might rather be a professional tennis player or a sponsored fly fisherman, enough other people are more skilled at those endeavors to match all the demand that exists. The professor’s comparative advantage is to teach engineering and economics to university students, because the professor can — theoretically — do that better than the other people who want to be professors.

The theory of comparative advantage doesn’t mean that every job is done by the person who can do it best. A professional tennis player might be a better engineering professor than the person who is actually an engineering professor. But the tennis player is making more money as an athlete, and their comparative advantage lies there. The athlete’s comparative advantage is playing tennis, and professor’s is being a professor. This is because the athlete’s opportunity cost is too high to be a professor.

Opportunity cost is the value of the next best alternative that is given up when a choice is made (Copilot 2023; Dictionary 2024). Take our scholar-athlete: if this person has exactly two choices in life (professor or athlete), then the opportunity cost of choosing to be an athlete is all the benefit they forgo by not being a professor including wages, the chance to work with students, and the thrill of learning new things.

Comparative advantage plays an important role in infrastructure, as it is the underlying process driving a great deal of the world’s transportation. Imagine a town with no transportation infrastructure: everything the town needs must be produced in the town. There will be lots of things that people in the town would want to buy, but there is no one with the time to produce it. But after engineers connect the town to the world economy by building ports, roads, railroads, airports, warehouses, and everything else, the comparative advantage changes. Suddenly goods that were expensive to produce in the town can be imported for a lower cost. This means that people can buy the cheaper goods, and the person who used to make those goods will find a new area in which he or she holds a comparative advantage.

Think

How does automation in manufacturing change an economy in the context of comparative advantage?

Example

Region $A$ can make cloth cheaply, but cannot produce dairy products like milk and cheese because the terrain is unsuitable for dairy farming. The 320,000 residents currently use 24,000,000 pounds of clothes which they make at $1.33 per pound, and 32,000,000 pounds of dairy products which they buy for $2.5 per pound.

Region $B$, on the other hand, has many high-quality dairy farms, but lacks the material necessary to produce clothing. The 400,000 residents currently buy 30,000,000 pounds of clothes for $2 per pound and produce the 40,000,000 pounds of dairy products they use for $1.5 per pound.

Currently, the two regions have no trade with each other. If a road were built between the regions, the cost of transporting dairy products would become $0.15 per pound, and $0.1 per pound of clothing. If the two regions began trading with one another, what would the economic benefits be for Regions $A$ and $B$?

The answer is found by comparing the regions’ current costs with their potential costs if they trade. Region $A$ can produce the clothing Region $B$ needs for much cheaper, and Region $B$ can provide the dairy products Region $A$ needs for less than their current costs. The cost of dairy in region $A$ before and after trade can be calculated as

\[\begin{align*} \text{Without trade:}& \ 32,000,000~lbs*\$2.5/lb&=\$80,000,000\\ \text{With trade:}& \ 32,000,000~lbs * \$(1.5+0.15)/lb&=\$52,800,000\\ \end{align*}\]

Region	Without Trade	With Trade	Benefits
A Dairy	$ 80,000,000	$ 52,800,000	$ 27,200,000
B Clothes	$ 60,000,000	$ 43,000,000	$ 17,000,000

This analysis shows that Region A would benefit $27,200,000 by trading with $B$ for dairy products instead of producing them internally. Similarly, Region B would gain a $17,000,000 benefit. Further, the benefits that go to consumers in Region A would be in addition to the extra business for producers (because the money consumers used to spend in Region B would be used to buy goods from Region B). Even though Region A gains more than Region B in this situation, both would be winners for working out this arrangement. Further, if the road costs less than $44.2 million to build, it makes economic sense to build it. It would be important to make sure that the costs are borne equitably between Region A and B, so that the system can be socially sustainable.

This example is drawn from Fricker and Whitford (2019), and used with permission.

3.2.1 Globalization

The benefits of comparative advantage are a driving force for globalization (Hayes 2025). Globalization is the process by which economies and systems are becoming more interconnected, across geographical and political barriers. As transportation and communications infrastructure improves, countries and individuals are more able to pursue their comparative advantage. This means that on average, people will be more wealthy. But some people may not benefit as much as others.

Figure 3.1: How globalization has materially affected people, or the elephant chart. From Marginal Revolution University

3.2.2 Tariffs

One way that countries attempt to address the negative impacts of globalization is through the use of tariffs. Tariffs are taxes imposed on goods produced in other countries. Tariffs in general reduce economic growth while raising prices, but there may be other reasons to have them. Radcliffe (2025) lists five reasons why governments impose tariffs:

Protect employment for certain sectors Research has shown that tariffs can protect employment in certain sectors, but there will be job losses in other sectors. For example, the US tariffs on Chinese steel and aluminum preserved jobs in the steel and aluminum industries, but it led to losses in exports as well as job losses in sectors that use steel and aluminum (Durante 2025).
National security In the event of a crisis, it may be difficult if your primary source of raw materials is imports from your adversaries. Steel and microchip production are often cited as industries that should be protected for national security reasons.
Protect consumers It may be that a government determines products made in another country pose risks to public health or safety but do not warrant a ban. A tarriff would encourage people to find cheaper — and presumably safer — substitutes.
Protect developing industries As industries start, foreign competitors may have manufacturing cost advantages. Solar panel and electric vehicle companies in the United States might be viable in the future, but not if they are smothered in their infancy by cheap foreign imports.
Retaliation Finally, governments use tariffs in retaliation for tariffs placed by other countries. After the US increased tariffs on Chinese steel, solar panels and aluminum, the Chinese government increased tariffs on US agricultural products including soybeans and cotton (Autor et al. 2024).

Think

We invest billions of dollars building infrastructure to facilitate world trade, and then we subsequently implement tariffs to restrict trade. Why do we do this?

3.3 Public and Common Goods

A good in an economy is something that can be owned or consumed by people; these can be actual products, or they can be services. Goods can be classified based on two primary characteristics:

Exclusivity: Can someone be effectively prevented from using a good if they did not pay for it?
Rivalry: Does using a resource prevent others from using it? Or does using it diminish the experience of others.

These two characteristics form a matrix of four types of goods, shown in Figure Figure 3.2. Private goods are rivalrous and exclusive. Most goods in the economy are like this. A grocery store requires that people pay for food before leaving with them (exclusive), and food that is consumed by one person is not consumed by other people (rivalrous). Goods that are exclusive but not rivalrous are sometimes called “club” goods: streaming services and cable internet are usually unaffected by the number of people watching them, but you have to have paid a login to get them.

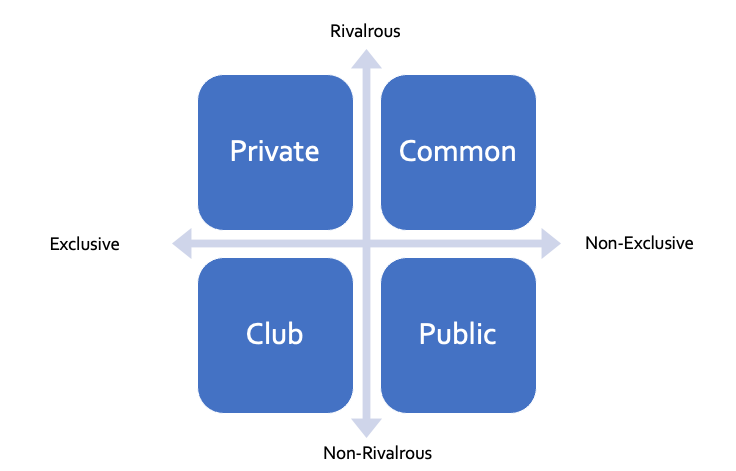
Figure 3.2: Types of goods by exclusivity and rivalry.

Public goods on the other hand are non-exclusive and non-rivalrous. A standard example of a public good is a light house. If you own a light house overlooking a harbor, there is no way for you to only allow ships that have paid a fee to see and use your light house (non-exclusive). If one ship is currently using your light house, other ships can use it at the same time (non-rivalrous). So if you own a light house, you probably need to find some other way to pay for your salary besides a subscription. In the United States, light houses are often operated by the Coast Guard as a public service.

In fact, much of the infrastructure in the United States is provided as a public good. Our lives are better and more prosperous because of this infrastructure, but it is sometimes hard to convince people to pay taxes to fund it.

Example

Consider two roommates who share certain household supplies like toilet paper and cleaning chemicals. These will be considered a “public good” that benefits both roommates. Roommate 1 has the following utility equation:

\[U_1 = \sqrt{x_1 + x_2} * \sqrt{y_1}\]

Where $x_1$ is the amount of shared supplies that Roommate 1 purchases, $x_2$ is the amount that Roommate 2 purchases, and $y_1$ is the amount of private goods that Roommate 1 purchases (foods, clothes, etc.). The budget for Roommate is given as

\[300 = 10x_1 + y_1\]

The combination of $x_1, y_1$ that maximizes Roommate 1’s utility subject to this budget constraint turns out³ to be a system of the following equations:

\[y_1 = 10(x_1 + x_2)\]

\[x_1 = 15 - x_2/2\]

If Roommate 2 buys more shared supplies, then the amount that Roommate 1 wants to buy goes down. If $x_2 = 20$, then $x_1 = 5$, and then $U_1 = \sqrt{25}\sqrt{250} = 79$. This is called the free rider problem.

But in reality, Roommate 2 is playing the same game, with an optimal $x_2 = 15 - x_1 / 2$. Solving the entire system together and calculating the utility, we get $U_1 = U_2 = \sqrt{10 + 10}\sqrt{200} = 63.2$

BUT

What if the roommates instead pooled their resources to buy the supplies? The two utility equations remain exactly the same, but the budget constraint is now

\[600 = 10x + y\]

In this case, it can be shown that the maximum utility point is at $y = 10x$. Putting this into the budget constraint gets us $x = 30, y = 300$, and the utility for each roommate is now $U_1 = U_2 = \sqrt{30}\sqrt{150} = 67.1$

So both roommates will have a higher utility (and be better off!) if they share resources and coordinate their purchase of public goods rather than compete with each other and hope the other guy pays.

Public goods are often owned by the public through governments, but not always. AM and FM radio and broadcast TV are all non-rivalrous and non-excludable. But just because they are public goods does not mean they are free; you pay to listen to the radio or watch TV by spending a good portion of your time in advertisements.

3.3.1 Tragedy of the Commons

Common goods are like public goods in that they are non-excludable. But common goods are rivalrous: not everyone can use the resource at the same time. Common goods can quickly become a sustainability issue. Usually, economists tend to believe that people following their own self-interest helps to set fair prices and encourages innovation and diversity in the economy. But if private interests encourage someone to over-use a common resource, then the resource could become degraded or disappear. This phenomenon — that private short-term interests conflict with long-term social interests — is called the tragedy of the commons.

The video below (or at this link) shows how the tragedy of the commons might play out in a village fishing pond; if people catch fish more quickly than they can regenerate, the pond will eventually have no fish. The public interest is in keeping the fish pond operating, but the private interest of each person is to catch as many fish as they can.

The Tragedy of the Commons can happen whenever private interests and public interests are in conflict. Examples or scenarios include the following:

Fisheries in the North Atlantic depleted by overfishing
Rain Forests destroyed for private agriculture
Excessive lumber extraction from national forests
Consuming irrigation water for high-water crops in California

Fixes for the Tragedy of the Commons usually require some kind of societal intervention. State fishing licenses limit the number of people who can fish, place catch limits on those who do, and provide resources for government enforcement and restocking efforts. Of course, knowing what interventions to install and how to shape them is a complicated problem.

think

Do we think of roads and streets as a private, common, or public good? Is this how they actually work? What are the consequences of this classification?

3.4 Externalities

Imagine you are riding your bicycle down a road when a large truck drives by “rolling coal”. As you inhale the noxious fumes, you suffer from this experience. And the truck drives on — perhaps oblivious to your coughing and perhaps not — without paying you anything for the costs his actions put on you.

It is common for the actions of one person to affect others. Sometimes these costs are captured within a market transaction, but other times they are not. Costs that are not captured within a transaction are called externalities because they are external to the transaction. When I put fuel in my gas tank and burn it, the market transaction is between me and the gas station / oil company. But everyone in the area breathes a little bit of my exhaust, and I’m not paying anyone to do that. Similarly, if I choose to stop buying gas and ride my bike, I still have to breathe the same polluted air as if I were driving.

So what can be done? In economic theory, the market sets the optimum cost of gasoline too low; the cost of pollution is not included in the transaction between the driver and the gas station. This means that there is some discrepancy between the market-established supply curve and a socially-optimal supply curve. If we implement a tax that moves the price of the from the the market price to the social optimum price, then the external costs can be captured and returned to the public.

Example

Demand for electricity is defined by the equation $D(Q) = 4/Q$. The market-determined supply function is $S(Q) = 1.2Q$, but the socially optimal supply function is $S'(Q) = Q^2$. Find the equilibrium price and quantity consumed under market the conditions and under socially-optimal conditions, and the tax required to acheive this optimum.

The market equilibrium can be found by setting $D(Q) = S(Q)$:

\[\begin{align*} 4/Q &= 1.2Q \\ Q^2 &= 3.33\\ Q &= 1.826\\ \end{align*}\]

implying that the equilibrium market price is $4/1.826 = 2.19$. The socially optimal equilibrium, however, is at $D(Q) = S'(Q)$:

\[\begin{align*} 4/Q &= Q^2 \\ Q^3 &= 4\\ Q &= 1.587\\ \end{align*}\]

and the equilibrium social optimum price is $4/1.587 = 2.52$. The tax should therefore be $2.52 - 2.19 = 0.33$

Unit Summary

A good introductory resource on many of the topics in this unit is Khan Academy’s Microeconomics course.

Economy The sum of all transactions in a society.
Supply The function relating the price of a good with the quantity produced by manufacturers.
Demand The function relating the price of a good with the quantity desired by consumers.
Opportunity Cost The cost of forgoing the next-best alternative among multiple options.
Utility The usefulness derived from purchasing goods and commodities; actors in the economy seek to maximize utility.
Money A medium of exchange that facilitates transactions.
Comparative Advantage A person’s or society’s ability to perform certain work more efficiently than another.
Public Good A non-exclusive and non-rivalrous good.
Common Good A non-exclusive but rivalrous good.

Homework

HW 1: Cement elasticity

Read this cement forecast for 2023, discuss why you think demand for cement is elastic or inelastic with respect to its price. Limit your response to 50 words.

HW 2: Elasticity

See the elasticity example above, near Equation 3.1. What would be the expected gallons per week of gas consumed if the gas price increased again to $3.15 and the elasticity remained the same?

HW 3: Supply and demand practice

Demand for a particular product can be described as $D(Q)=1000 − Q$ and supply as $S(Q)=200 + 5Q$ for prices between $200 and $1000.

What is the equilibrium quantity and price demanded.
Suppose that demand is expected to increase in proportion to population growth. What will be the equilibrium quantity and price in 10 years if the population grows by 10%?
Suppose that over the same period, a new technology allows suppliers to cut their marginal costs to $3 per unit. That is, the supply function changes from $S(Q)=200 + 5Q$ to $S(Q)=200 + 3Q$. What is the new equilibrium quanity, and what is the new equilibrium price? (Assume that demand has also grown by 10%, as in part 2.)

HW 4: Nonlinear Supply and Demand

Assume the same price range of $200 to $1000, as in the problem above, but this time demand can be modeled as $D(Q)=(-975(Q-1245))^{1/2}$ and supply as $S(Q)=100*\ln(Q-150)/\ln(2)$. Make a rough sketch of the resulting graph, and solve for the equilibrium price and the quantity produced using a graphing calculator or other numerical / computer-based tool.

HW 5: Roads and the tragedy of the commons

Using the definition of a public good, are public roads a public good? Why or why not? What does this mean for highway infrastructure in the US?

HW 6: Air pollution and externalities

⁴One major element of air pollution is the concentration of particles in the atmosphere that are smaller than $2.5\mu m$; when this concentration reaches more than $35 \mu g / m^3$, breathing becomes hazardous for people with asthma or other respiratory conditions. Utah already regularly exceeds EPA minimum standards for particulate matter pollution. A primary contributor to particulate matter pollution is vehicles, through exhaust and also the microscopic pieces of rubber that rub off when tires roll on pavement.

Consider that aggregate demand for vehicle travel can be represented with the function $p = 0.89 * \exp(-0.04 * q)$ where $p$ is the price of car travel per mile in dollars, and $q$ is million vehicle miles traveled (MVMT). Consider that the supply function of gasoline, tires, insurance, etc. is given by the function $p = 0.08 * \exp(0.06*q)$. Find the equilibrium price and quantity in dollars and MVMT.
An analysis determines that to protect public health, aggregate VMT has to be reduced to at most 20 million. What tax on car travel per mile would accomplish this?
Consider that by 2050, the population in Utah County is expected to double ($D_{2050} = 2D_{2020}$). What would be the equilibrium price and total VMT if the tax is not implemented?
What would the VMT tax need to be to keep aggregate VMT under 20 million in 2050?
Consider the global, economic, environmental, and social implications of the proposed VMT tax. Create a table categorizing who and what will benefit if Utah imposes the VMT tax, and who or what will benefit by not imposing the tax.
Informed by the previous analysis, how do you propose that Utah County responsibly use the revenues generated by the VMT tax?

Alternative translations of this are very helpful for understanding the meaning. See, for instance BibleHub ↩︎
subsidized heavily by tax payers or private donors in most cases, especially at BYU.↩︎
Using a bit of multivariable calculus↩︎
This homework assignment is used to evaluate ABET Student Outcome 4.↩︎